Geometri Derslerinden Hatırladığımız ‘Özel Üçgenler’ ve Özellikleri
Eğer üniversitede ilgili bir bölüm okumuyorsanız ya da işinizde aktif olarak kullanmıyorsanız üçgenler ile en son lise sıralarında geometri dersi alırken karşılaşmışsınızdır. Matematik ve geometri genel olarak ülkemizde pek sevilmeyen alanlar oldukları için aslında bu derslerde gördüğümüz üçgen ve benzeri şekillerin hayatın pek çok farklı noktasında karşımıza çıkıyor olduğunu kolay kolay fark etmeyiz.
Elbette bu yazımızda hayatın içindeki üçgenlerden değil, geometri alanındaki üçgenlerden bahsedeceğiz. Bazı üçgenler açı dereceleri ve kenar uzunlukları bakımında sabittir. Bu üçgenler, özel üçgenler olarak adlandırılırlar. Her birinin kendine ait değişmez kuralları ve bazı önemli özellikleri vardır. Gelin özel üçgenler nelerdir yakından bakalım ve her birinin öne çıkan özelliklerini görelim.
Özel üçgenler nelerdir?
Açılarına göre özel üçgenler 30 – 60 – 90 üçgeni 30 – 30 – 120 üçgeni 45 – 45 – 90 üçgeni 15 – 75 – 90 üçgeni Kenarlarına göre üçgenler 3 – 4 – 5 üçgeni 8 – 15 – 17 üçgeni 5 – 12 – 13 üçgeni 7 – 24 – 25 üçgeni İkizkenar üçgen Eşkenar üçgen Üçgenler hakkında bilmeniz gerekenler

Açılarına göre özel üçgenler
30 – 60 – 90 üçgeni 30 – 30 – 120 üçgeni 45 – 45 – 90 üçgeni 15 – 75 – 90 üçgeni
30 – 60 – 90 üçgeni
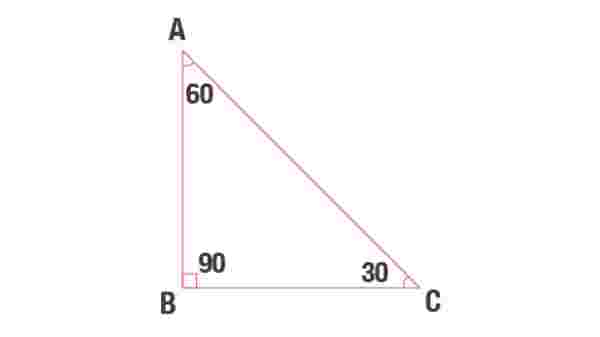
30 – 60 – 90 üçgeninde üçgenin bir köşesinin açısı 30 derece, bir köşesinin açısı 60 derece, bir köşesinin açısı ise 90 derecedir. 90 derecelik açıya sahip olan köşenin karşısındaki kenar hipotenüstür. Bu kenar, üçgenin en büyük kenarıdır çünkü üçgendeki en geniş açılı köşeye bakmaktadır.
30 – 30 – 120 üçgeni
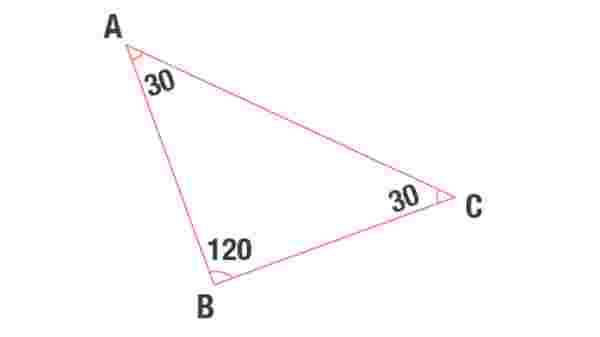
30 – 30 – 120 üçgeninde üçgenin bir köşesinin açısı 30 derece, bir köşesinin açısı da 30 derece, bir köşesinin açısı ise 120 derecedir. 30 – 30 – 120 üçgeninde geniş açının karşısındaki kenarı bulma yöntemi farklıdır. Bu üçgende, 30 derecelik açıya sahip olan köşelerin karşısındaki kenarların √3 değeri hesaplanır. Bu hesap sonucunda elde edilen değer, karşı kenardır.
45 – 45 – 90 üçgeni
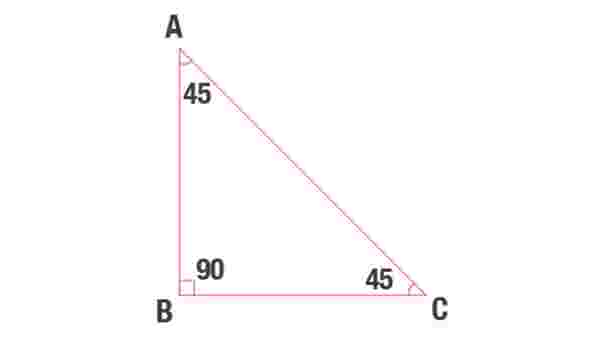
45 – 45 – 90 üçgeninde üçgenin bir köşesinin açısı 45 derece, bir köşesinin açısı da 45 derece, bir köşesinin açısı ise 90 derecedir. 45 – 45 – 90 üçgeninde de farklı bir hipotenüs bulma yöntemi kullanılır. Bu üçgende, 45 derecelik açıya sahip olan köşelerin karşısındaki kenarların √2 değeri hesaplanır. Bu hesap sonucunda elde edilen değer, hipotenüstür. 45 – 45 – 90 üçgeni, bir ikizkenar üçgendir.
15 – 75 – 90 üçgeni
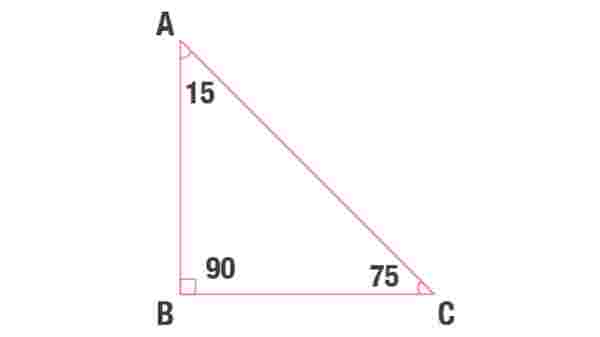
15 – 75 – 90 üçgeninde üçgenin bir köşesinin açısı 15 derece, bir köşesinin açısı 75 derece, bir köşesinin açısı ise 90 derecedir. 15 – 75 – 90 üçgeninde de farklı bir hipotenüs bulma yöntemi kullanılır. Bu üçgende hipotenüs, üçgen yüksekliğinin dört katıdır. 15 – 75 – 90 üçgeni, bir dar açılı üçgendir.
Kenarlarına göre üçgenler
3 – 4 – 5 üçgeni 8 – 15 – 17 üçgeni 5 – 12 – 13 üçgeni 7 – 24 – 25 üçgeni İkizkenar üçgen Eşkenar üçgen
3 – 4 – 5 üçgeni
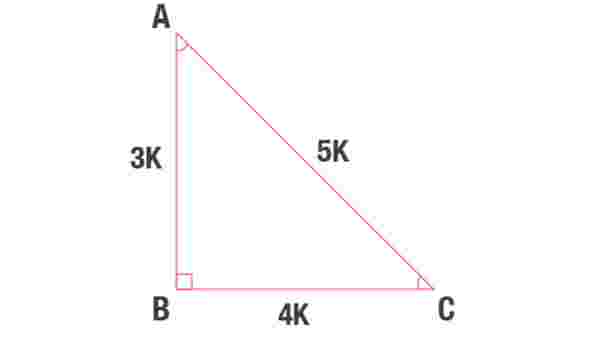
3 – 4 – 5 üçgeninde üçgenin bir kenarının uzunluğu 3 ve 3’ün katları, bir kenarının uzunluğu 4 ve 4’ün katları, bir kenarının uzunluğu ise 5 ve 5’in katları şeklindedir. Uzunluk ölçüleri ne olursa olsun 3 – 4 – 5 üçgeninde uzunluklar hep bu rakamların katlarıdır. 3 – 4 – 5 üçgeninde açılar; 36,87 derece, 53,13 derece ve 90 derecedir.
8 – 15 – 17 üçgeni
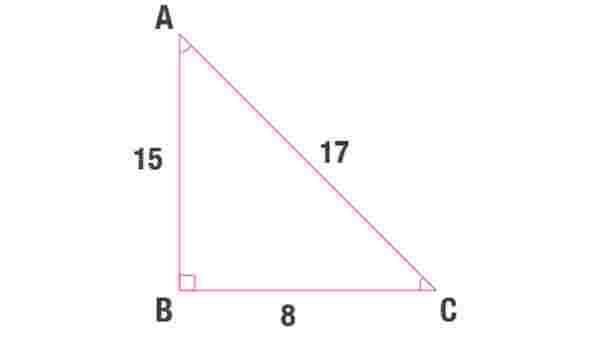
8 – 15 – 17 üçgeninde üçgenin bir kenarının uzunluğu 8 ve 8’in katları, bir kenarının uzunluğu 15 ve 15’in katları, bir kenarının uzunluğu ise 17 ve 17’nin katları şeklindedir. Uzunluk ölçüleri ne olursa olsun 8 – 15 – 17 üçgeninde uzunluklar hep bu rakamların katlarıdır.
5 – 12 – 13 üçgeni
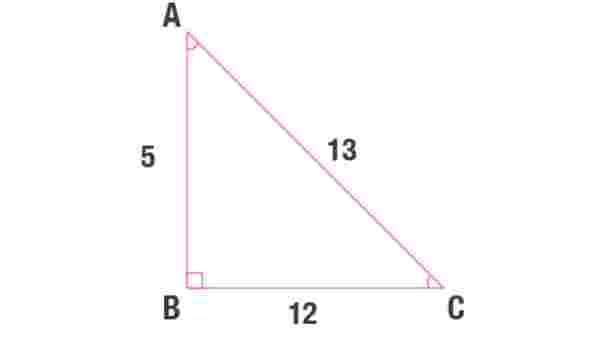
5 – 12 – 13 üçgeninde üçgenin bir kenarının uzunluğu 5 ve 5’in katları, bir kenarının uzunluğu 12 ve 12’nin katları, bir kenarının uzunluğu ise 13 ve 13’in katları şeklindedir. Uzunluk ölçüleri ne olursa olsun 5 – 12 – 13 üçgeninde uzunluklar hep bu rakamların katlarıdır.
7 – 24 – 25 üçgeni
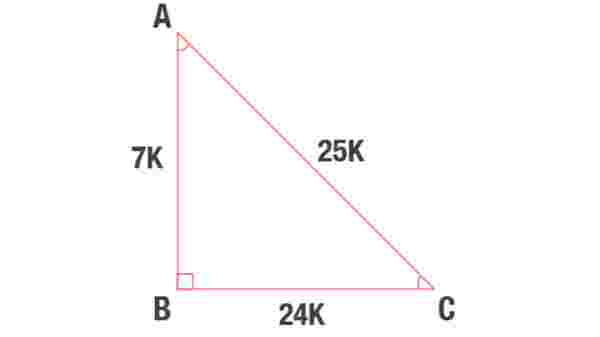
7 – 24 – 25 üçgeninde üçgenin bir kenarının uzunluğu 7 ve 7’nin katları, bir kenarının uzunluğu 24 ve 24’ün katları, bir kenarının uzunluğu ise 25 ve 25’in katları şeklindedir. Uzunluk ölçüleri ne olursa olsun 7 – 24 – 25 üçgeninde uzunluklar hep bu rakamların katlarıdır.
İkizkenar üçgen
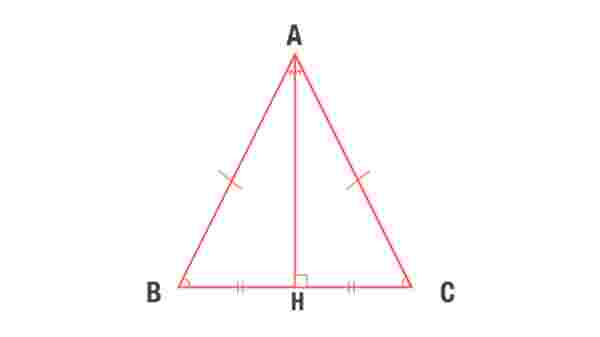
Bir üçgeni alın ve hem açıortayı hem de kenarortayı eşit iki parçaya bölecek şekilde bir dik indirin. Sonuçları hesapladığınız zaman ortaya çıkan kenarlar birbirine eşit çıkıyorsa elinizde bir ikizkenar üçgen var demektir. Yine bir üçgeni alın ve tabandan iki kenara doğru iki paralel çizgi çizin. Bu paralellerin uzunluklarını toplayın. Yapılan işlem sonucu bir kenarın uzunluğuna eşit olduğunu göreceksiniz.
Eşkenar üçgen
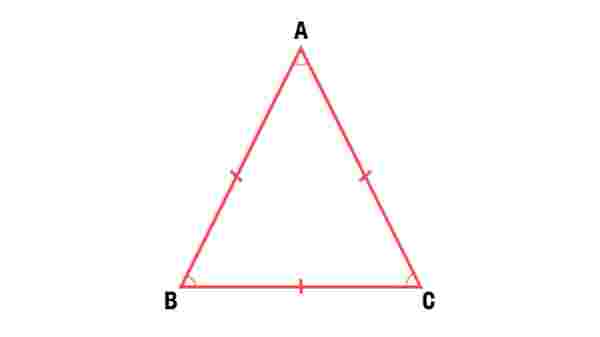
Bir üçgenin tüm kenarları eşitse bu üçgen, eşkenar üçgen olarak adlandırılır. Eşkenar üçgenin bir köşesinden dik bir çizgi indirerek bir yükseklik oluşturduğunuz zaman bu yükseklik, hem kenarortay hem de açıortay oluşturur.
Üçgenler hakkında bilmeniz gerekenler:
Artık hepimizin ezberlediği gibi bir üçgenin iç açıları toplamı 180 derecedir. Köşeleri A, B ve C olarak adlandırılan bir ABC üçgenini ele aldığımız zaman, bu üçgenin A noktasından teğet geçen ve BC köşelerine paralel olan bir dik çizersiniz BC doğrusunun açıları, bu doğru parçasının yarısını kaplayacaktır. Bir üçgenin herhangi bir dış açısını hesaplamak için o dış açıya komşu olmayan diğer iki iç açıyı toplamanız yeterli.
Yukarıda detaylarını verdiğimiz özel üçgenler alt başlıklar olarak eşkenar üçgen, ikizkenar üçgen, çeşitkenar üçgen, dar açılı üçgen, dik açılı üçgen, geniş açılı üçgen gibi farklı isimler alırlar. Üçgen hesaplamaları için bazı bağıntılar vardır. Bunlar pisagor teoremi, kenardan yararlanma yöntemi, açıdan yararlanma yöntemi, heron yöntemi, kosinüs teoremi, öklit bağıntısı gibi farklı isimlerle anılırlar.
Köşe, kenar, iç açı, dış açı, derece, uzunluk gibi temel elemanların yanı sıra üçgenlerde bir de açıortay ve kenarortay olarak anılan iki farklı yardımcı eleman bulunmaktadır. Üçgenlerin ortaya çıkardığı farklı açılar ve uzunluklardan oluşan geometrik şekilleri incelemek için pek çok farklı teorem vardır. Bunlar arasında en bilinenler Ceva Teoremi, Menelaus Teoremi, Steward Teoremi ve Carnot Teoremidir.
Geometrinin en bilinen konularından bir tanesi olan ve hayatın hemen her alanında karşımıza çıkan özel üçgenler nelerdir sorusunu yanıtlayarak bu özel üçgenlerin özelliklerinden ve genel olarak üçgenler hakkında bilmeniz gereken detaylardan bahsettik.
